Проективография...

• Текст:В. Н. Гамаюнов
  7 ноября 2025
• Добавить в кабинетДобавлено в кабинет

С абстрактными представлениями геометрических фигур, их измерением и способами отображения человек уже сталкивался на заре своего развития — при выделке орудий труда, изготовлении различной утвари, обработке полей и постройке жилищ. Авторы известной «Истории математики»» в подтверждение этого повествуют, что «...уже в глубокой древности изготавливались скребки и ножи в форме дисков, треугольников, ромбов и сегментов, круглые сосуды; поля имели форму прямоугольников, а здания форму конуса, цилиндра и параллелепипеда». А это и есть процесс формирования «азбуки и словаря» абстрактных символов, которые несмотря на внешнюю размерную схожесть с соответствующими вещами предметного мира, как бы возвышались над ними, отличаясь абстрактными признаками, которые- то и формировали наши идеальные представления об устройстве материальных вещей и происходящих с ними явлений. Так появился мир абстрактных вещей — алфавит, цифровые знаки, геометрические фигуры и т. п., которые имели и обратную связь — то есть влияли на формирование нового мира предметных вещей. Ель похожа на конус, но конус становился похожим на шатровую башню. Ровная площадь земли похожа на геометрическую плоскость, а та в свою очередь порождает наши представления о наиболее ровной плоскости лезвия инструмента, который использовался для разрезки различных материалов... Подобно тому, как шло абстрактное формирование литер и составляемых из них слов в словесном языке, вылившееся в эпоху Возрождения в книгопечатное дело, шло формирование и учения об абстрактных фигурах и их пропорциях, о перспективном отображении. Именно перспектива, родившаяся в эпоху Возрождения, так же сыграла роль графической «грамматики» для последующего развития проектной графической «письменности» архитектора, художника и нынешнего дизайнера. Этой «грамматикой» до сих пор пользуются все деятели пластических искусств.

Но многие абстрактные знания формотворчества, как и сами акции формотворчества, в наш век преданы анафеме. А наиболее признанная их часть в сталинский период была посрамлена и подвергнута критиканству. Тогда одно упоминание авангардизма и вообще всего нового в пластических искусствах было таким же тяжким преступлением, как, например, принадлежность к партии эсеров или меньшевиков. И вот что удивительно при этом — пересекались и прекрасно сосуществовали две диалектические противоположности: поиски нового и преклонение перед памятниками старины. Казалось бы, столь различные вещи! Поощрялся примитивизм голой и длительно необозримой плоскости с лозунгами и цитатами о светлом будущем. Особой привилегией пользовались те художники, которые во имя собственного блага нанимались в оранжереи угоднического искусства и создавали «летопись больших и малых вождей», указующих путь в это светлое будущее. И во исполнение этих задач сметалось все, что казалось помехой, что не удовлетворяло тщеславия и капризов таких художников. Кстати — и памятники древней старины. В вакханалии разрушения памятников архитектуры, да и всей материальной культуры, организованной «вождем всех времен и народов», превращались в руины не только храмы, культовые изделия, но уничтожались и люди, священники и мастера, которые были причастны к их созданию и сохранению. Не уцелели и секреты их создания, чертежи и технологии. Акты вандализма коснулись и самой теории, которая превращалась в прах и тлен. Зашторивались все извечные знания о красоте, особенно те, которые проливали свой яркий свет из эпохи Возрождения. В их числе и наиболее устойчивые математические знания о фигурах и пропорциях — они просто оплевывались. Посрамлялась, например, так называемая божественная пропорция золотого сечения. Объявлялась никчемной геометрия луковичных церквей. И чуть было не подобрались даже к уничтожению шатровых башен московского Кремля и даже к филигранным луковицам самого Василия Блаженного.

Но вот в их-то построении заключалась иная логика пространственного мышления, незапечатленная ни в каких математических книгах. Логика и порожденная ею красота форм, перед которой дрогнул даже Наполеон Бонапарт, остановившийся на Красной площади в своем походе на Россию. Но эта логика, как стало нам известно, весьма отличается от традиционной логики ортогонального мышления, которая была взята, несмотря на свой пластический примитив, на вооружение всеми последующими «завоевателями» после Наполеона. Особенно в этом ортогональном мышлении преуспели те, кто создавал «архитектуру» ГУЛАГов и фашистских концлагерей.

В противовес такой «ортогональной болезни» формотворчества и порожденному ею пластическому миру вещей кое-где в мире (США и Канада) к середине XX века начались поиски новых путей формотворческой деятельности. В результате этого появились сложнейшие пластические решения в купольной архитектуре (Фуллер Р. Б.), а затем — столь же сложная филигрань звездчатых многогранных форм (Кокстер Г. М.). Они постепенно подвели нас к осознанию качественно новых геометрических моделей пространства, которые сейчас принято называть структурами. Было, в частности, осознано, что структуры строятся на основе известных групп симметрии путем всевозможных объединений и пересечений известных геометрических моделей. Была так же осознана многовариабельность различных пластических решений в одной и той же ткани структурного пространства. Эта многовариабельность особенно усиливалась его бесчисленными модификациями проективного преобразования. Такие преобразования, между прочим, подвели нас к осознанию совершенно нового метода отображений — проективографического метода, который лишен был двух важных недостатков ортогонального метода. Мы имеем в виду недостоверность (искаженность) отображения элементов пространства, которые не принадлежат прямоугольной системе плоскостной квантификации пространства, и практическую невозможность в одних и тех же проекциях представлять различные пластические решения формы.

С появлением проективографии мы устранили эти недостатки, но приобрели некое новое качество научного мышления, которое никак не объяснялось только проективными методами преобразований. И это качество нами было постепенно осознано. Природа его происхождения наконец-то прояснилась путем привлечения комбинаторного мышления, которое предполагает изучение всех возможных перестановок пространственных элементов. Ведь до сих пор, кроме того, что комбинаторное преобразование существует, например, в шахматах, никто толком не знал: в каком порядке элементы (например, горошины) из мешка гороха могут перейти на плоскость, запакетированную ими. Но поиски велись. На их пути была изобретена важнейшая пространственная игра «Кубик Рубика», наглядно продемонстрировавшая разрывность элементов (кубичков) при различных операциях комбинаторного преобразования. Но это была лишь прелюдия. Здесь мы научились переставлять элементы из одного места пространства в другое. В проективографии нам удалось осмыслить более серьезно все эти операции (а это случилось раньше, чем была изобретена игра «Кубик Рубика»), когда в процессе их выполнения автору статьи удалось перешагнуть ранее запретный барьер при переходе из трехмерного пространства в двухмерное, то есть при отображении пространства на поле чертежа. Этим был найден ключ к расшифровке проективографических отображений, в «памяти» которых удерживались многовариантные пространственные пластические решения формообразования.

Найденный ключ вначале помог расшифровать три классических ткани пространства (тетраэдрическую, октаэдрическую и икосаэдрическую). Он подходил одинаково ко всем. Точно так же позднее А. С. Близнюком были расшифрованы гиперпространства, которые происходили от антипризм и бипирамид. Оставался открытым только один вопрос — сколько же существует таких пространственных модификаций, в которых действуют комбинаторные операции перестановок? Но этот вопрос решается не комбинаторикой, а классической теорией групп. Имеется в виду — групп пространственных симметрий, о разновидностях которых мы мало еще что знаем. Вот почему мы обязаны пригласить всех исследователей к этой сложнейшей проблеме. А пока мы можем подробно рассказать о том, что нам удалось сделать в известных пространствах, показать их проективографические изображения и приемы формообразующей деятельности.

Чтобы заинтересовать читателя этой проблемой, мы вначале покажем плоды формотворчества на основе проективографии, а затем расскажем об основных секретах формотворческих акций, предназначенных для их создания.

Построение проективографических полей

В настоящее время построение различных проективографических полей (чертежей) по трем произвольно выбранным точкам (в условиях определенного ограничения, о котором будет сказано ниже) осуществляется компьютерными способами, для чего программистом А. В. Иващенко (Моспроект-3) разработаны соответствующие программы. Однако эти способы проистекают из геометрических построений, которые легко осуществить ручным способом (при помощи циркуля и линейки). Но они имеют свою геометрическую специфику. Остановимся на ней кратко, но вполне достаточно для тех, кто пожелает построить проективографическое поле собственными руками.

Во-первых, любую из здесь приводимых проективографических эпюр проще задать не тремя точками, а тремя произвольно выбранными отрезками, обязательно образующими остроугольный треугольник. Это и есть то единственное ограничение, которое накладывается на этот произвольный выбор трех элементов на плоскости. Такие три стороны некоторого остроугольного треугольника и будут первыми тремя линиями (за исключением простейшего театраэдрического поля) будущей проективографической эпюры. Дело в том, что на тетраэдрическом поле эти три линии мнимые (они нужны лишь для последующего построения). На более сложных полях — октаэдрическом и икосаэдрическом эти линии остаются действительными.

Во-вторых, в компьютерных программах для построения названных полей используются соответствующие алгоритмы, представляющие либо пропорцию математического гармонизма (условно назовем «серебром»), либо пропорцию золотого сечения (условно назовем «золотом»). В соответствии с избранием одной из этих пропорций идет пересечение трех избранных линий всеми последующими (искомыми). Ведь точки пересечения образуют отрезки (на этих первоначально заданных линиях), находящиеся в соответствующей пропорциональной зависимости. Так, для отрезков тетраэдрического и октаэдрического поля — это «серебро», а для отрезков икосаэдрического поля — это «золото». Но заметим, что упомянутые пропорции представляются для компьютера в качестве числовых алгоритмов, хотя они проистекают из обычных геометрических построений. Такими построениями являются построения подсистем осей симметрии Платоновых тел (тетраэдра, октаэдра или икосаэдра). Напомним, что подсистемой осей симметрии мы называем не все оси выбранного платонового тела, а лишь те, которые принадлежат одной его зеркальной плоскости. Если в разных зеркальных плоскостях Платонова тела (как это имеет место у октаэдра) два различающихся вида расположения осей симметрии, то говорят о наличии двух подсистем. Тетраэдр и икосаэдр имеют по одной подсистеме осей.

Выстраивая соответствующие подсистемы и встраивая в них выбранные три отрезка остроугольного треугольника, можно геометрическим способом (при помощи циркуля и линейки) получить те же пропорциональные деления. Поэтому желающим избежать алгебры можно предложить следующие геометрические построения.

Способы построения подсистем осей симметрии могут быть традиционными, то есть осуществляться через ортогональные проекции соответствующих Платоновых тел (рис. 1 — для тетраэдра, рис. 2, 3 — для октаэдра, рис. 4 — для икосаэдра). Поскольку конструкторы и дизайнеры владеют начертательной геометрией, знания которой необходимы для этих построений, то наша помощь в их описании необязательна. Однако для икосаэдра можно предложить нетрадиционный способ, разработанный автором, который представляется более простым. Остановимся на его описании.

Зададимся в начале задачей построить четвертую часть сектора подсистемы осей симметрии икосаэдра. Это построение представлено поэтапно на рисунках 5 и 6. Здесь первоначально задаются ортогональные оси окружности. На вертикальной оси от центра устанавливают отрезок произвольной величины а. Из этого же центра проводят окружность радиусом 1,5 a. Тогда вписанный в эту окружность прямоугольник со стороной отсекает на диаметре отрезок b. Отложив на этом же диаметре примыкающий к нему отрезок 2b, получаем ряд четырех точек A, B, C и D. Соединив их с вершиной О, получаем искомую четвертую часть сектора осей симметрии. Дополнив ее соответствующими зеркальными отражениями относительно сторон этого сектора, получим полную подсистему шести осей симметрии (см. рис. 4) икосаэдра.

Построив выбранную подсистему (для октаэдра — пару подсистем), можно приступить к заданию в ней сторон некоторого остроугольного треугольника. Здесь необходимо заметить, что задаваемые отрезки в подсистеме, как правило, остроугольного треугольника не образуют — они разомкнуты. Это происходит потому, что любая подсистема может рассматриваться как совмещение всех аналогичных (накладывающихся на нее) подсистем пространства. В результате же такого совмещения происходит расслаивание линий пересечения подсистем (плоскостей) на пары линий. Поэтому примыкающие в пространстве две стороны искомого треугольника в одной вершине «расслаиваются» на пары вершин. Вспомните, что такое же расслоение испытывают вершины следов плоскости общего положения в эпюре Монжа по известной оси y. Здесь же идёт расслоение иногда по всем трем осям. Этот механизм «расслоения» определяется дуговыми линиями связей. Отсюда и обратный процесс — реконструкция по ним искомого треугольника, результаты которой можно видеть на начальных стадиях построения эпюр. Здесь важно заметить, что реконструируется не только искомый треугольник, но и все точки (будущих пересечений его сторон с другими линиями), которые возникают в чертеже подсистемы в результате пересечения с соответствующими осями симметрии.

При последовательном построении проективографических полей приводимых видов рекомендуется проводить его в два этапа.

Первый из них предполагает знание конструктивных особенностей строения избранного вида эпюры, то есть взаимного расположения и числовых значений ее основных точек и линий, без чего невозможно построение всего поля. Такие основные совокупности точек и линий мы называем основной конфигурацией данного проективографического поля. Во второй части статьи (см. следующий номер «ТЭ») мы покажем эти конфигурации в качестве начального построения соответствующих эпюр при задании некоторого исходного остроугольного треугольника. Построить каждую из таких конфигураций не представляет никаких сложностей, если вы сможете однажды запомнить ее зрительный образ. Как и любая простейшая конфигурация (треугольник, квадрат, пятиугольник и т. п.), эти конфигурации характеризуются определенным числом точек, линий и, например, входящих в их состав остроугольных треугольников. Помимо этого, каждая точка такой конфигурации снабжается числовыми значениями проходящих через нее плоскостей, что указывает на ее связи с другими множествами элементов пространства. Именно эти числовые значения определяют места пересечения соответствующих плоскостей пространства с полем чертежа, то есть все остальные линии эпюры. При этом необходимо иметь в виду, если при данной точке конфигурации стоит, например, цифра 6, то это означает: через нее проходит ров-но 6 плоскостей и ровно на одну меньше их линий пересечения (с полем), так как плоскость чертежа сама с собой пересечься не может.

Дальнейшее построение эпюры, когда основная конфигурация готова, связано с отысканием конкретно именованных линий, проходящих через определенную точку конфигурации. Здесь-то и наступает второй (завершающий) этап построения проективографического поля.

Чтобы его реализовать, необходимо прежде всего дать определенные наименования всем плоскостям пространства, которые взаимодействуют с полем чертежа. При этом условимся эпюрную плоскость называть цифрой 1, а все остальные — другими цифрами, как это показано на соответствующих развертках Платоновых тел (рис. 7, 8 и 9). В дальнейшей работе эти развертки рекомендуется склеить (рис. 10, 11, 12). Здесь уместно отметить принятую условность: обозначенные цифрами части (треугольники) поверхности Платоновых тел и их соответствующие проективографические поля в общем случае не совпадают, однако последние имеют те же наименования. Такая условность обеспечивает все возможные случаи рубки пространства проективографическими полями в избранной системе симметрии, что дает возможность получить все возможные проективные модификации соответствующего вида решетки пространства.

Используя принятые наименования всей системы плоскостей пространства (избранного вида), необходимо выявить их первичные симметричные объединения, которые пересекаются в определенных точках проективографического эпюрного поля. Эти группы плоскостей называются коническими группами симметрии. Такие группы плоскостей пересекаются в вершине некоторого конуса, которая принадлежит эпюрной плоскости. При этом необходимо иметь в виду, что от каждой такой вершины (а она есть точка основной конфигурации эпюры) в пространство уходит ось симметрии конуса, вокруг которой транслируется эпюрная плоскость. Число таких трансляций определяет порядок симметрии данной конической группы.

Определить наименования плоскостей, входящих в данную коническую группу, не представляет никакой сложности. Для этого достаточно выбрать на макете какую-нибудь ось симметрии (например, симметрию восьмого порядка, проходящую через вершину треугольника 1) и отыскать соответствующую ей эпюрную точку. После чего на поле эпюры выписываются при данной точке соответствующие наименования плоскостей названной группы симметрии (эти наименования: 1, 2, 3, 4, 5, 6, 7, 8). Таким образом, через определившуюся точку пройдут семь линий с соответствующими наименованиями (за исключением наименования 1). Точно так же отыскиваются наименования групп симметрии при других точках конфигурации, после чего пары точек с одинаковыми наименованиями соединяются. Заметим, что при наличии параллельных плоскостей (например, 2 и 47, что обнаруживается в макете) появляется возможность проведения искомой линии через одну точку.

При завершении построения эпюры необходимо иметь в виду плоскости, которые не проходят через точки основной конфигурации, но они в каких- то точках пересекают ее основные линии, образуя при них группы симметрии четвертого порядка. Их так же отыскивают по макету.

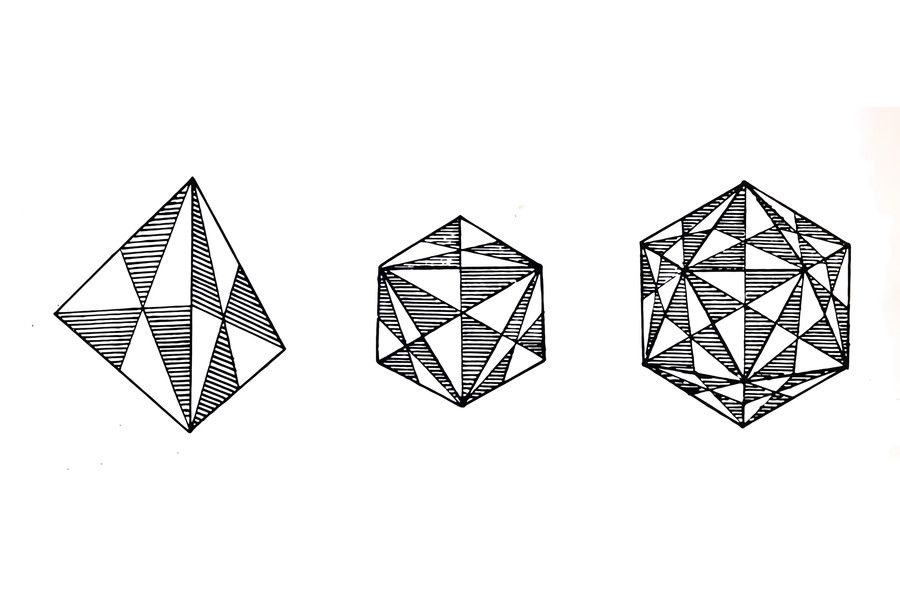
В итоге всех этих рекомендованных процедур и построений должны получиться эпюры трех видов: тетраэдрическая, октаэдрическая и икосаэдрическая. Каждая из них соответственно должна иметь 23, 46 и 118 линий (рис. 13). Картины расположения этих линий в общем виде — неправильные, так как происходят от некоторого неправильного остроугольного треугольника. Однако, если внимательно присмотреться к этим более общим конфигурациям, то в них можно обнаружить некоторые черты правильности. Так вы найдете пары линий, которые одинаково разделены, то есть могут быть совмещены друг с другом. Существуют одинарные линии, как результат совмещения пар одинаково разделенных линий. Если такие линии снабдить соответствующими указателями (например, дужками поворота и т. п.), то можно приступить к чтению этих загадочных эпюр.